All posts by Walter Frei
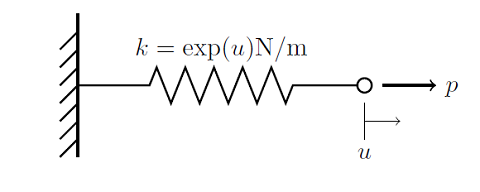
Solving Nonlinear Static Finite Element Problems
Here, we begin an overview of the algorithms used for solving nonlinear static finite element problems. This information is presented in the context of a very simple 1D finite element problem, and builds upon our previous entry on Solving Linear Static Finite Element Models.
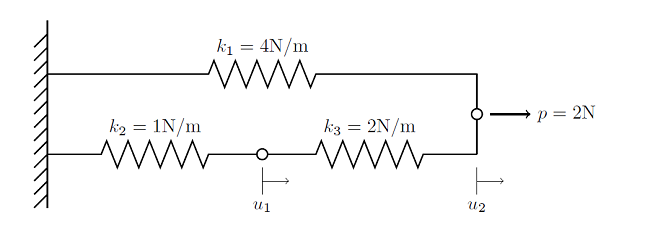
Solutions to Linear Systems of Equations: Direct and Iterative Solvers
In this blog post we introduce the two classes of algorithms that are used in COMSOL to solve systems of linear equations that arise when solving any finite element problem. This information is relevant both for understanding the inner workings of the solver and for understanding how memory requirements grow with problem size.
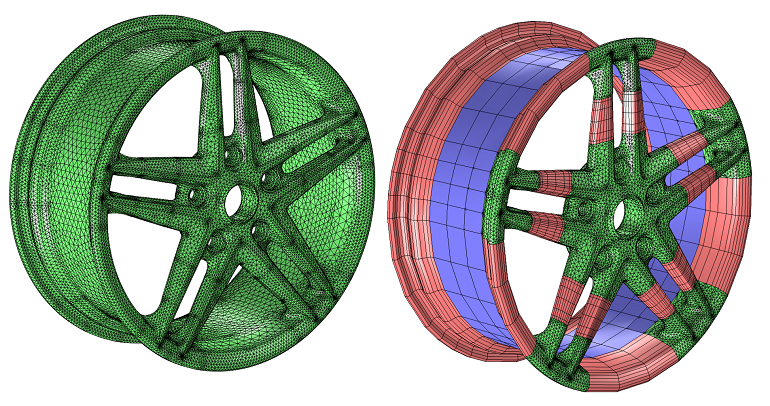
Meshing Your Geometry: When to Use the Various Element Types
In a previous blog entry, we introduced meshing considerations for linear static problems. One of the key concepts there was the idea of mesh convergence — as you refine the mesh, the solution will become more accurate. In this post, we will delve deeper into how to choose an appropriate mesh to start your mesh convergence studies for linear static finite element problems.
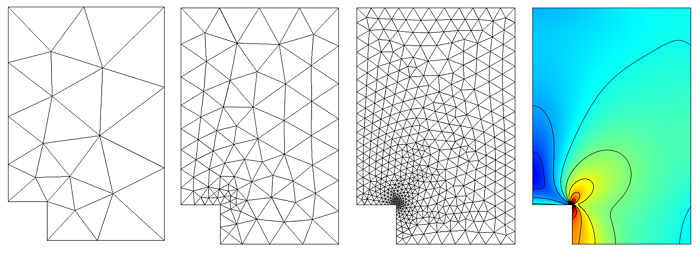
How to Identify and Resolve Singularities in the Model when Meshing
In our previous post on Meshing Considerations for Linear Static Problems, we found that, in the limit of mesh refinement, the solution to the finite element model would converge toward the true solution. We also saw that adaptive mesh refinement could be used to generate a mesh that would have smaller elements in regions where the error was higher, rather than simply using smaller elements everywhere in the model. In this post, we will examine a couple of common pitfalls […]
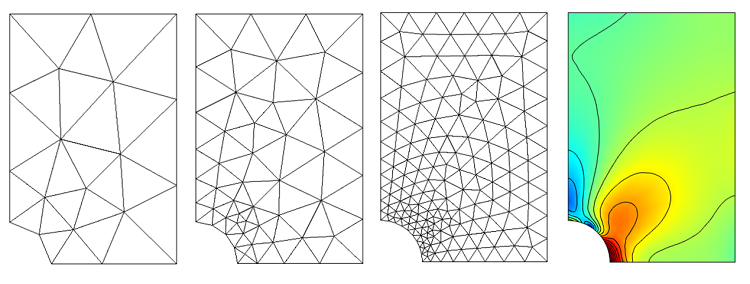
Meshing Considerations for Linear Static Problems
In this blog entry, we introduce meshing considerations for linear static finite element problems. This is the first in a series of postings on meshing techniques that is meant to provide guidance on how to approach the meshing of your finite element model with confidence.

Solving Linear Static Finite Element Models
In this first blog entry of our new solver series, we describe the algorithm used to solve all linear static finite element problems. This information is presented in the context of a very simple 1D finite element problem, but is applicable for all cases, and is important for understanding more complex nonlinear and multiphysics solution techniques to be discussed in upcoming blog posts.
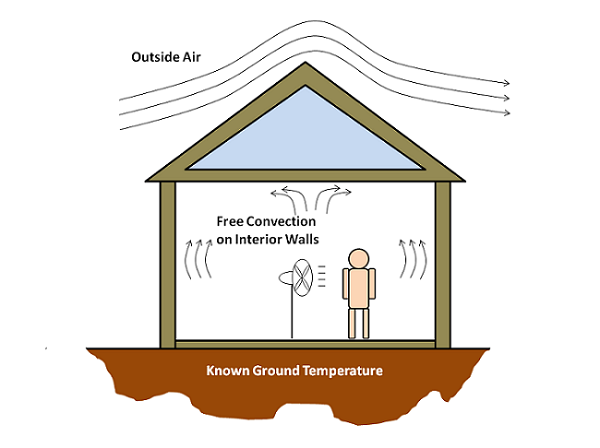
Using Global Equations: Modeling Room Air Temperature in a House
An interesting question came up the other day that I felt would make an excellent blog post since it allows us to discuss one of the very powerful, and often underutilized, features of COMSOL Multiphysics: the Global Equation. In this post, we will look at using global equations to introduce an additional degree of freedom to a model. This additional degree of freedom will represent something we do not want to model explicitly.
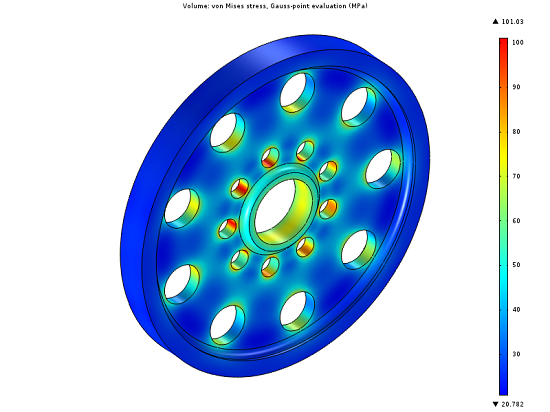
Using Gradient-Free Optimization
The COMSOL Optimization Module includes both gradient-based and gradient-free optimization techniques. Whereas the gradient-based optimization method can compute an exact analytic derivative of an objective function and any associated constraint functions, it does require these functions to be smooth and differentiable. In this blog post, we examine the use of the gradient-free optimizer, which can consider objective function and constraints that are not differentiable or smooth. The dimensions of a spinning wheel are optimized to reduce the mass while maintaining […]
