Equation-Based Modeling Blog Posts

Understanding Stabilization Methods
When modeling transport applications driven by convection, you need a stabilization method — whether you’re working with finite elements, finite volumes, or finite differences.
How to Integrate Functions Without Knowing the Limits of the Integral
Did you know that the COMSOL® software can solve integrals as well as partial differential equations? Learn how to integrate functions — even without knowing the limits of the integral.

The Strength of the Weak Form
Learn about the origins of the weak form equations, how to derive them from classic equations, how to express them in the COMSOL Multiphysics® syntax, and more >>
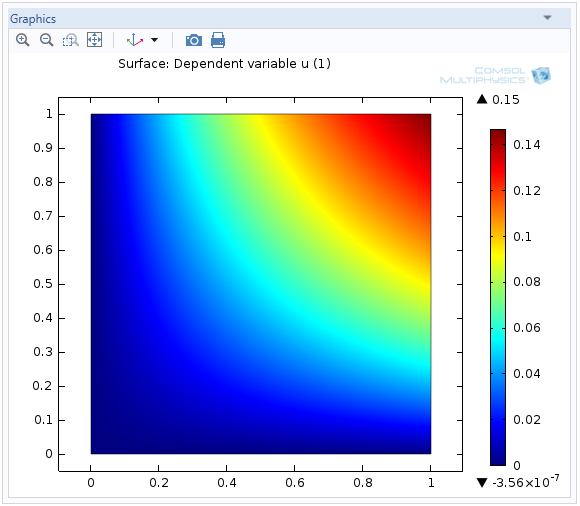
Solving Algebraic Field Equations
COMSOL Multiphysics® is commonly used to solve PDEs, ODEs, and initial value problems. However, did you know that you can also solve algebraic and even transcendental equations?
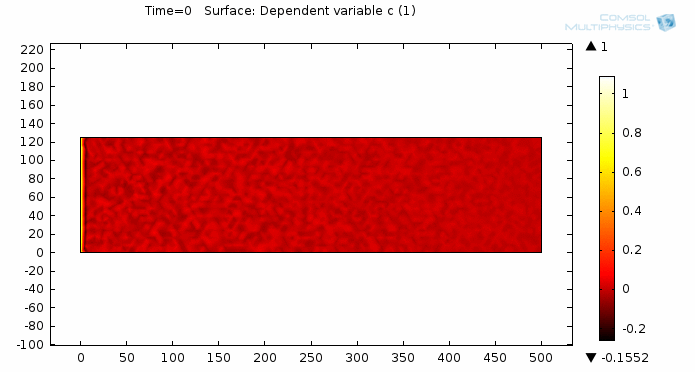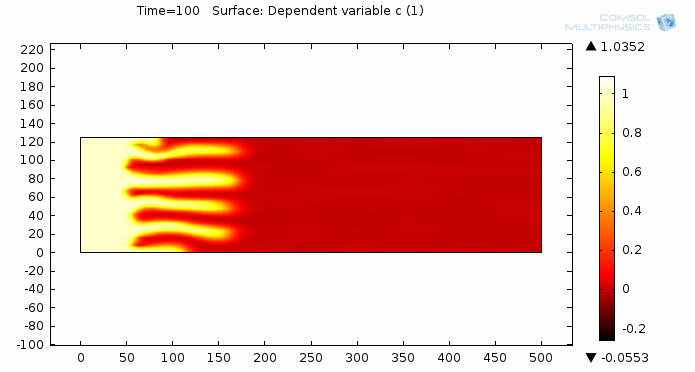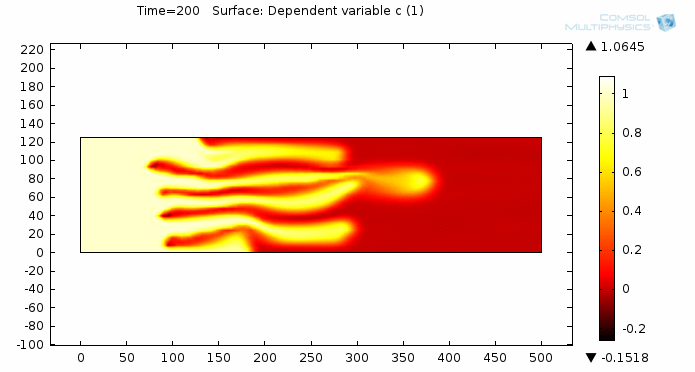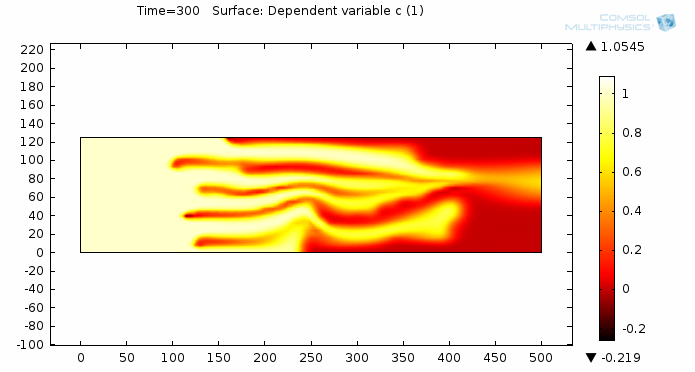
Simulating Viscous Fingering Using Equation-Based Modeling
A prospective user of COMSOL approached me about modeling viscous fingering, which is an effect seen in porous media flow. He hadn’t found a satisfying solution elsewhere, so he turned to COMSOL. I’d like to share with you some of my insight on how to go from idea to model to simulation by taking a “do-it-yourself approach” and utilizing the equation-based modeling capabilities of COMSOL Multiphysics.
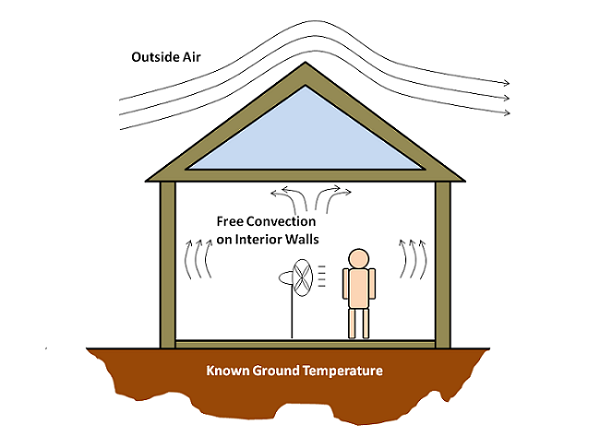
Using Global Equations: Modeling Room Air Temperature in a House
An interesting question came up the other day that I felt would make an excellent blog post since it allows us to discuss one of the very powerful, and often underutilized, features of COMSOL Multiphysics: the Global Equation. In this post, we will look at using global equations to introduce an additional degree of freedom to a model. This additional degree of freedom will represent something we do not want to model explicitly.
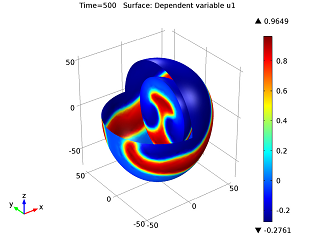
Equation-Based Modeling, a Custom Model of a Beating Heart
Equation-based modeling is one of the great strengths of COMSOL Multiphysics. The ability for you to easily access the equations describing the physics you are working with, and adding or manipulating them as you see fit, dramatically opens up the realm of possibilities that you can achieve through modeling and simulation. This is exemplified by the following custom model of a beating heart.
Equations: Who Needs Them?
Most of us take mathematical modeling for granted. After all, we’re taught physics and calculus almost hand-in-hand. But we owe a lot to the early pioneers like Isaac Newton, who demonstrated and strongly promoted interpreting natural phenomena through equations. Differential equations are especially useful since most things change as time marches on. Since we live in 3D space, partial differential equations (i.e., equations that express change in more than one “direction”) arise as the prominent tool to express continuum level […]
