General Blog Posts
Multiphysics Simulation Is More Accessible with the Application Builder
Simulation experts can design user-friendly, specialized simulation apps with the Application Builder. Read what engineers and professors from around the world have to say about this tool here.

Generating Animations to Visualize Your Simulation Results
Why create animations from your COMSOL Multiphysics® simulation results? We share 4 reasons in this blog post.

Using the Domain Decomposition Solver for Thermoviscous Acoustics
Learn how to use the Domain Decomposition solver, a memory-efficient iterative algorithm with inherent parallelism on the geometric level, in COMSOL Multiphysics®.

How to Analyze Your SOLIDWORKS® Designs with an App
Combining the power of a CAD design tool with a simulation app in the same modeling environment enables the simulation to work with both in synchronicity. Learn how to do so here.

Using the Domain Decomposition Solver in COMSOL Multiphysics®
The Domain Decomposition solver is a memory-efficient iterative algorithm that works best for large modeling problems that can’t be solved with other direct or iterative methods.
Improve the Productivity and Safety of a Perforated Well with an App
Perforated wells offer a viable approach for recovering oil and gas trapped in reservoirs. See how apps can help speed up the design process of these devices…
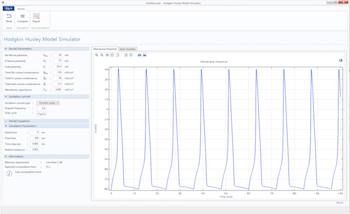
Analyze the Hodgkin-Huxley Model with a Computational App
The Hodgkin-Huxley model is an advanced model for simulating action potential. We also go over how to use a computational app to streamline this type of analysis.
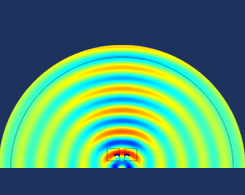
How to Use Acoustic Topology Optimization in Your Simulation Studies
Today, guest blogger René Christensen of GN Hearing discusses the importance of acoustic topology optimization and how to apply it in COMSOL Multiphysics. Topology optimization is a powerful tool that enables engineers to find optimal solutions to problems related to their applications. Here, we’ll take a closer look at topology optimization as it relates to acoustics and how we optimally distribute acoustic media to obtain a desired response. Several examples will further illustrate the potential of this optimization technique.
