Equation-Based Modeling Blog Posts
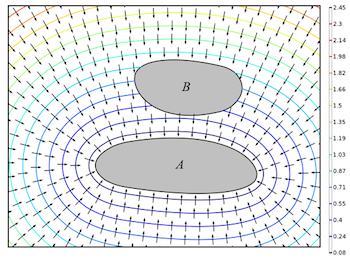
How to Compute Distances Between Objects in COMSOL Multiphysics®
Compute the distance between two deforming objects in the COMSOL Multiphysics® software. Here’s how…

Solving Shallow Water Equations with Equation-Based Modeling
Shallow water equations are an example of equation-based modeling. You can define expressions in COMSOL Multiphysics® to solve a shallow water equation for coastal erosion analyses.
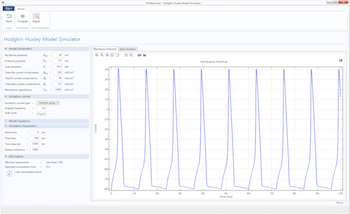
Analyze the Hodgkin-Huxley Model with a Computational App
The Hodgkin-Huxley model is an advanced model for simulating action potential. We also go over how to use a computational app to streamline this type of analysis.

Understand the Dynamics of the FitzHugh-Nagumo Model with an App
In 1961, R. Fitzhugh and J. Nagumo proposed a model for emulating the current signal observed in a living organism’s excitable cells. This became known as the FitzHugh–Nagumo model.
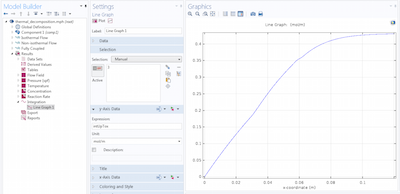
Integrals with Moving Limits and Solving Integro-Differential Equations
Learn how to analyze spatial integrals over variable limits, whether they are prescribed explicitly or defined implicitly. (Part 2 of 2)
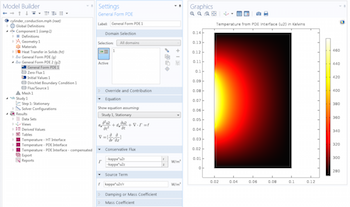
Guidelines for Equation-Based Modeling in Axisymmetric Components
Here’s your comprehensive guide to equation-based modeling for problems with cylindrical coordinates and axisymmetric components.

Investigating Turing’s Theory of Morphogenesis
Ever wonder how a tiger gets its stripes? Alan Turing’s theory of morphogenesis explains how patterns, such as stripes, develop naturally from initially homogeneous states.
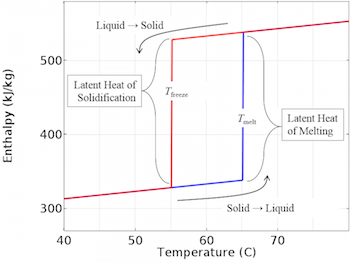
Thermal Modeling of Phase-Change Materials with Hysteresis
Hysteresis occurs when the melting temperature of a material is different from the solidification temperature. We demonstrate the thermal modeling of such a material here.
