To help optimize your modeling processes, we are continuously striving to enhance the quality of our meshing capabilities. The recent improvements to the algorithm for generating tetrahedral meshes in the COMSOL Multiphysics® software are one such example. Follow along as we guide you through the process of generating a tetrahedral mesh to highlight this improved functionality and its correlating features, while discussing its role in helping you obtain better simulation results.
The Demands of a Mesh Generator
The demands of a mesh generator can be quite extensive. The generated mesh, for instance, must conform to the geometry as well as create elements of the most optimal sizes and shapes. Elements where the edges and angles between them are close to being equal in size provide a greater chance of reaching solution convergence as well as more accurate results. Further, the generator may have to grade over short distances to create very small elements in tight spaces and very large elements in more open spaces without creating problems in the solution algorithms. Finally, it should be preferable that the generator acts automatically and works for all types of geometries.
Every meshing operation in COMSOL Multiphysics creates a mesh that conforms to the respective geometry. But the tetrahedral mesh generator, which operates under the Free Tetrahedral node in the Model Builder, is the only mesh generator in 3D that is fully automatic and can be applied to every geometry. And since it creates an unstructured mesh — that is, a mesh with irregular connectivity — it is well suited for complex-shaped geometries requiring a varying element size. Since tetrahedral meshes in COMSOL Multiphysics are used for a variety of physics, including multiphysics, the mesh generator needs to be very flexible. It should be possible to generate very fine meshes, very coarse meshes, meshes with fine resolution on curved boundaries, meshes with anisotropic elements in narrow regions, etc.

A tetrahedral mesh of a gas turbine.
Thanks to recent updates in COMSOL Multiphysics, you can now achieve improved quality in your tetrahedral meshing and thus advance the reliability of your simulation results. To demonstrate this, let’s walk through the steps of generating a tetrahedral mesh.
Generating a Tetrahedral Mesh in COMSOL Multiphysics®
Most tetrahedral mesh generators fall into one of the following three classes:
- Advancing front-based generators, which pave the domain with tetrahedra, adding them one by one beginning from a boundary
- Octree-based generators, which first decompose the domain with an octree and then partition each octree cell into tetrahedra
- Delaunay-based generators, which maintain a geometric structure called the Delaunay tetrahedralization of the domain and have remarkable mathematical properties
The tetrahedral mesh generator in COMSOL Multiphysics is a Delaunay-based mesh generator. As a Delaunay mesher, the process of generating a tetrahedral mesh can be divided into the five main steps described below. The third and fifth step of the meshing process have been significantly improved with upgrades to COMSOL Multiphysics version 5.2a. To illustrate the different steps, we’ll use a very coarse mesh of the piston geometry, which is available in the meshing tutorials of the Application Library within COMSOL Multiphysics.

The geometry of the piston_mesh application.
1. Generating the Boundary Mesh
If you monitor the Progress window when building a tetrahedral mesh, you can see that the first 35% of the progress is devoted to the generation of the boundary mesh. But creating a boundary mesh that is well suited for the subsequent steps of the tetrahedral mesh generation process is not a straightforward task. There are several issues that must be addressed, such as:
- Adjusting the element size according to curved boundaries as well as distances between edges/faces across faces/domains
- Smoothly propagating the element size throughout the geometry
- Detecting self-intersecting edge and face mesh elements and resolving these problems
- Dealing with poorly parameterized CAD surfaces
- Dealing with virtual geometry definitions
- Creating high-quality triangles
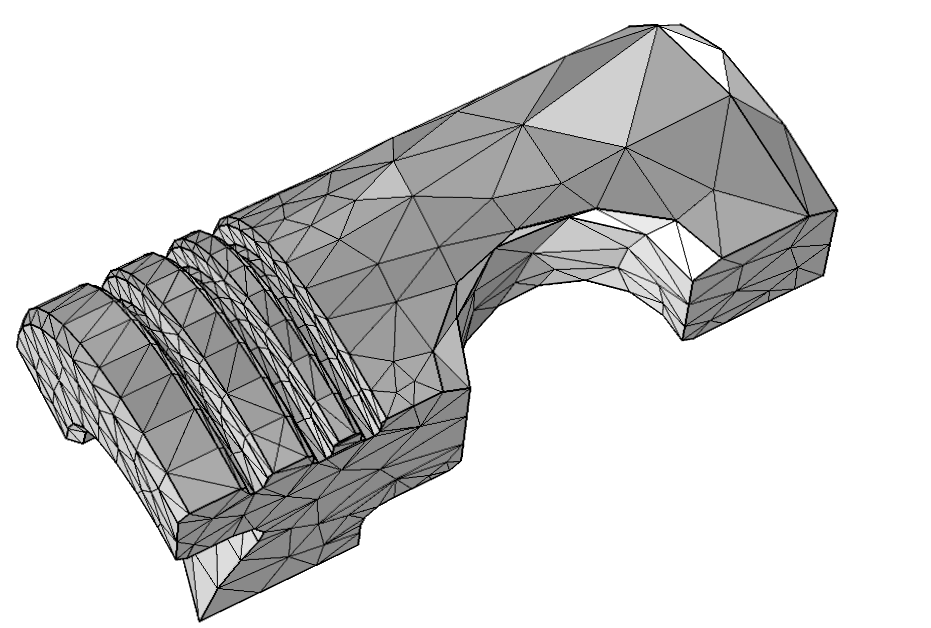
The boundary mesh for the piston_mesh application using the element size Extremely Coarse.
2. Creating Delaunay Tetrahedralization of the Boundary Mesh Points
The next step is to create the Delaunay tetrahedralization of the boundary mesh points, which form the convex hull of these points. These are also a set of points that have some nice mathematical properties, such as that no point of the point set will be placed inside the circumsphere of any tetrahedron. In 2D, the Delaunay triangulation of a set of points maximizes the minimum angle of all the angles of the triangles in the triangulation, although this property does not apply in 3D. Yet, there is no guarantee that the edge and triangle elements of the boundary mesh exist as edges and triangles in the Delaunay tetrahedralization of the boundary mesh points — not even for a convex boundary mesh. We will deal with this in the following step.
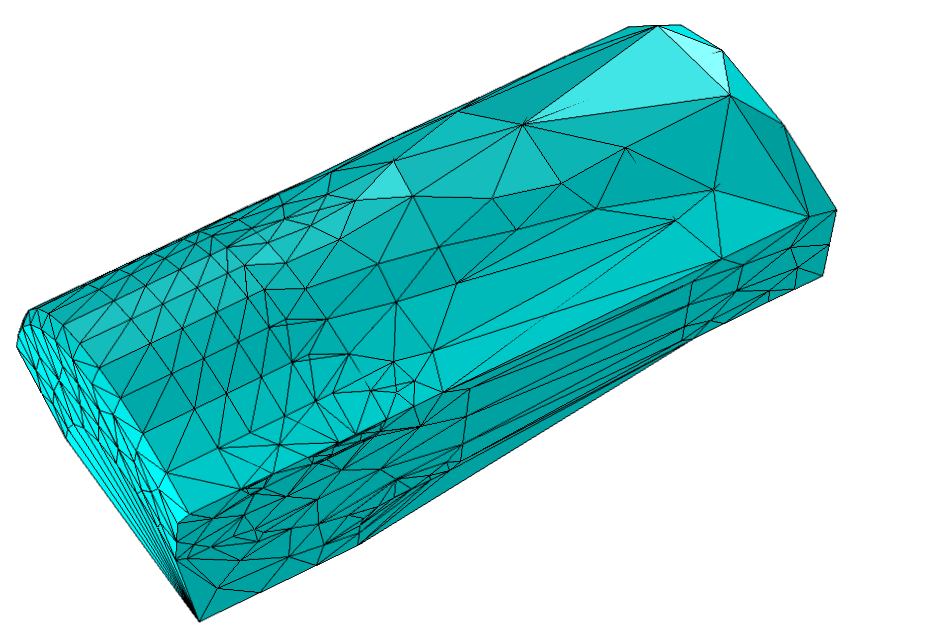
The Delaunay tetrahedralization of the boundary mesh points forming the convex hull of the points.
3. Conforming the Delaunay Tetrahedralization to the Boundary Mesh
So far, we have generated the final boundary mesh and a Delaunay tetrahedralization of the boundary mesh points. Here, we will enforce the edges and triangles of the boundary mesh into the tetrahedralization. This is the most demanding part of the entire meshing process.
Last year, we released a completely new algorithm to account for this step, and the algorithm was significantly improved in COMSOL Multiphysics version 5.2a. In earlier versions, when meshing complex geometries, you may have received error messages like “failed to respect boundary element edge on geometry face” or “internal error in boundary respecting”. Such failures originated from this part of the meshing process. With the new improvements, it is possible to safely remove all tetrahedra on the outside of the boundary once all of the edges of the boundary mesh have been enforced into the tetrahedralization, and all of the tetrahedra intersecting the triangles of the boundary mesh have been addressed.
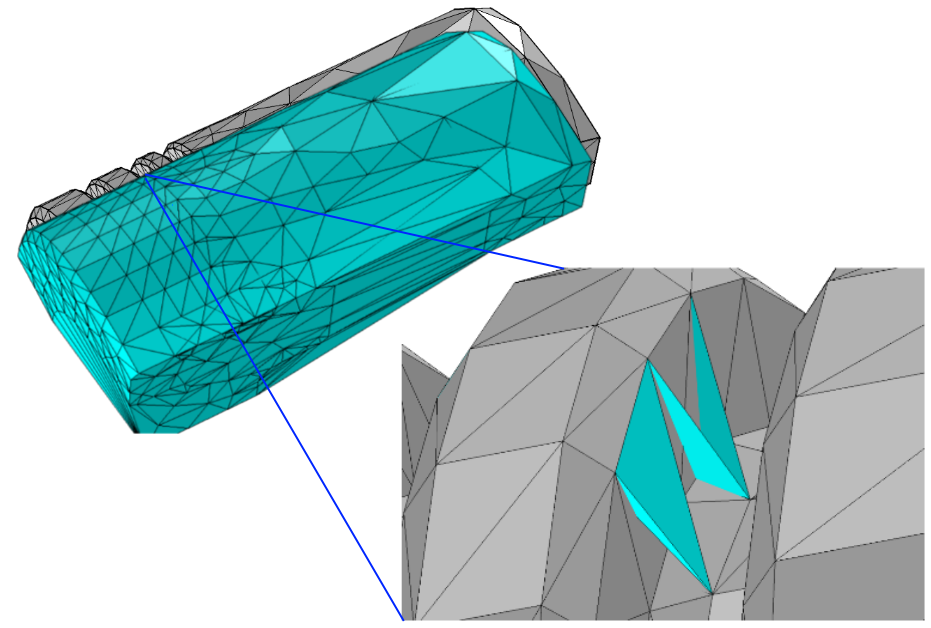
The upper left part of the figure shows the boundary mesh in gray and the Delaunay tetrahedralization of the boundary mesh points in cyan. The zoomed view in the lower right part of the figure shows a few of the hundreds of tetrahedra that intersect edges and triangles of the boundary mesh. In this step, the tetrahedralization is modified such that no tetrahedron intersects the boundary mesh. Some additional points (so-called Steiner points) might be inserted to achieve a boundary conforming tetrahedralization.
4. Refining the Boundary Conforming Tetrahedralization by Inserting Interior Points
Now that we have a tetrahedralization across the entire geometry, with the boundary mesh from the first step serving as an outer boundary, we still have a tetrahedralization that does not contain any interior points (except the Steiner points that may have been added previously). Our next task is to refine the tetrahedralization by inserting points in the interior until the specified element size is achieved everywhere. The points can easily be inserted using a regular Delaunay refinement scheme. Some special treatment is needed though as at this stage, the tetrahedralization does not fulfill the Delaunay properties everywhere.

The upper left part of the figure shows a cut through of the tetrahedralization after the third step, with only a few interior points inserted during that part of the meshing process. The lower right part of the figure shows the same cut through the tetrahedralization after the fourth step, where the tetrahedralization fulfills the element size specification also in the interior of the domain.
5. Improving the Quality of the Refined Tetrahedralization
At this point, we are almost done. But before we return the mesh to the user, we need to first improve the quality of the tetrahedra. Each tetrahedron can be assigned a quality value in the range of 0 to 1. A regular tetrahedron has a quality of 1 and a totally flat tetrahedron has a quality of 0. COMSOL Multiphysics version 5.2a delivers a new algorithm that further improves the quality of the meshes. The algorithm also features an option for reducing the risk of obtaining inverted curved elements as well as an option for avoiding the creation of elements that are too large.
In this step, we will increase the quality of the worst elements such that the quality of the mesh, which is largely dictated by the quality of its worst elements, is sufficiently good for a typical simulation. The new algorithm has a broader palette of operations for improving the quality of the mesh including point relocation (often referred to as smoothing) and topological modification operations such as edge and face swapping, edge collapsing, and vertex insertions. By applying these operations repeatedly, an infinite number of unique tetrahedralizations can be reached for a domain defined by its boundary mesh, which means a mesh with better quality will always exist. However, for a given tetrahedralization where the minimum element quality cannot be improved by smoothing, it’s not obvious which topological operation to perform to improve the quality. Sometimes even a series of operations must be applied — vertex insertion followed by edge flipping and smoothing — before you can reach an optimized mesh.
There are three optimization levels included in the algorithm: Basic, Medium, and High. These levels determine the amount of effort put into the optimization process. Say, for instance, you build your mesh using the Basic option (the default) and encounter problems with convergence when computing the solution or perhaps reduced accuracy in your results due to a poor quality mesh. In this case, you can rebuild your mesh with a higher optimization level to get a better chance at convergence with better results.
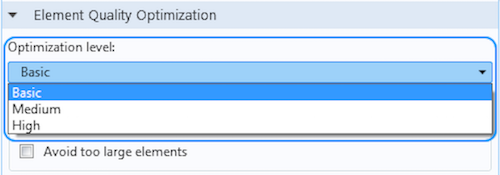
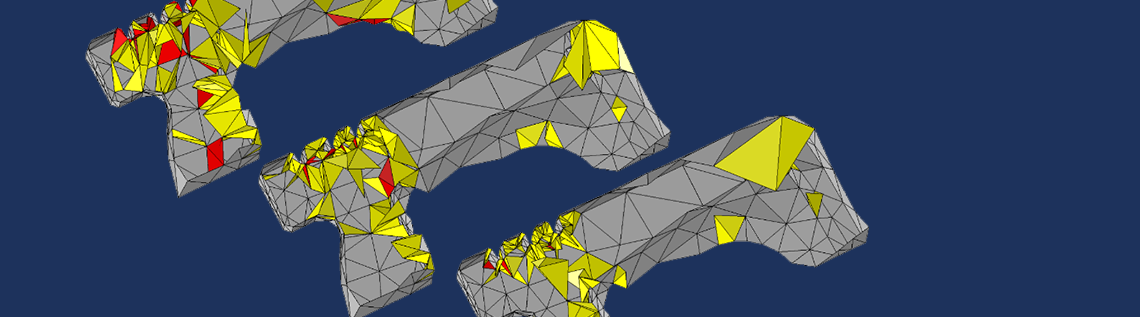
The quality improvement algorithm offers three levels of optimization (Basic, Medium, and High) that determine how much effort is put into the optimization process.
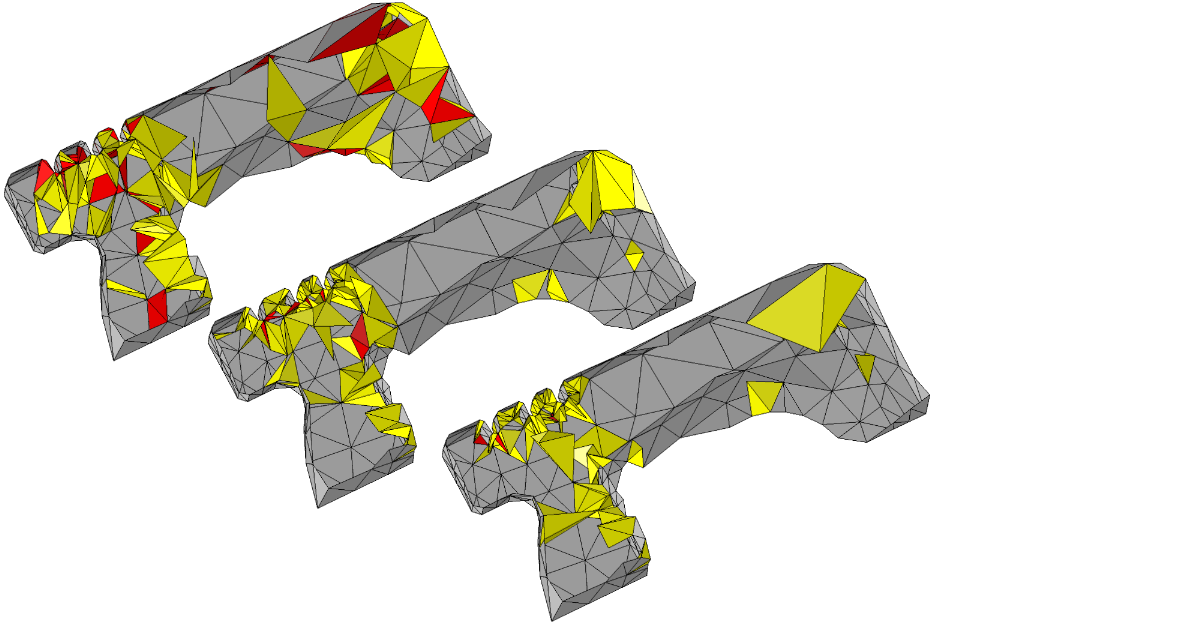
These mesh cut throughs show the elements with the lowest quality before optimization (upper left), with the optimization level set to Basic (middle), and with the optimization level set to High (lower right). The red tetrahedra have a quality value less than 0.1, while the yellow tetrahedra have a quality value between 0.1 and 0.25. The gray triangles define the mesh cut through’s boundary mesh.
The algorithm also offers two options for reducing the risk of obtaining inverted curved elements as well as reducing the size of the largest tetrahedra. Note that these selections come at the cost of a longer meshing time and slightly lower element quality.
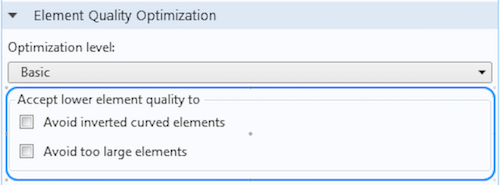
If the geometry includes fillets or other curved regions with a relatively coarse mesh, and you solve with a geometry shape order higher than one, you can select the Avoid inverted curved elements check box. This will let the optimization algorithm try to reduce the number of mesh elements that become inverted when they are curved. If the computation is sensitive to mesh elements that are too large, you can select the Avoid too large elements check box in an effort to avoid generating tetrahedra that are larger than the specified element size.
Improving Our Tetrahedral Mesh Generator to Meet Your Simulation Needs
Mesh generation is a concept that is rather easy to understand: It is all about partitioning a geometry into pieces of linear shape. There are, however, some difficulties to address when it comes to generating a tetrahedral mesh for simulation purposes. There will always be challenging geometries for which the generator fails or gives a mesh with elements that are of a lower quality. But with recent improvements to the tetrahedral mesher in COMSOL Multiphysics, you can now better address such complex geometries and further advance your modeling processes for continued optimization.
Find Out More About the Meshing Capabilities of COMSOL Multiphysics®
- Browse other posts on the COMSOL Blog relating to the topic of meshing
- Head over to our Video Gallery to check out videos that show you how to utilize meshing features and functionality in COMSOL Multiphysics



Comments (0)