Blog Posts Tagged Technical Content
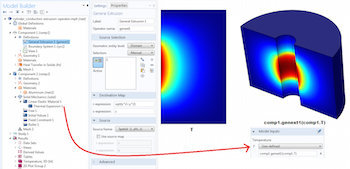
Part 2: Mapping Variables with General Extrusion Operators
Learn how to use the General Extrusion operators, which are designed to handle nonlinear mappings and the mapping of variables between geometric entities of different dimensions. Part 2 of 2.
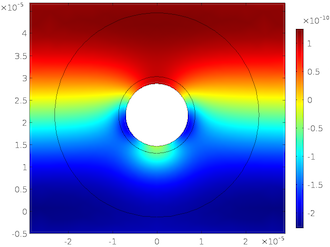
A Thermoviscous Analysis of Acoustic Radiation Forces
Learn how to determine acoustic radiation forces, including thermoviscous and acoustophoretic effects, in the COMSOL® software.
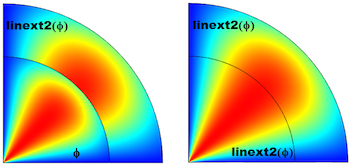
Accessing Nonlocal Variables with Linear Extrusion Operators
In some modeling scenarios, you may need to transfer variables from one region of a computational domain (the source) to another (the destination). This can be done with an extrusion operator.

Finding a Structure’s Best Design with Topology Optimization
Think about the first architects who designed a bridge above water. The design process likely included several trials and subsequent failures before they could safely allow people to cross the river. COMSOL Multiphysics and the Optimization Module would have helped make this process much simpler, if they had computers at the time, of course. Before we start to discuss building and optimizing bridges, let’s first identify the best design for a simple beam with the help of topology optimization.

What Is Geometric Nonlinearity?
If you perform structural mechanics analyses, then you have most likely encountered the concept of geometric nonlinearity. But what exactly does geometric nonlinearity mean?

How to Improve Your Paddle Stroke with Simulation
To take a closer look at a paddle stroke, for activities like canoeing and dragon boat racing, we set up a 2D model in COMSOL Multiphysics® and visualize the flow pattern around the paddle blade.

Deformed Mesh Interfaces: Rotations and Linear Translations
Using the finite element method often involves modeling solid objects that are rotating and translating within other domains. See how to use the deformed mesh interfaces to model these movements.
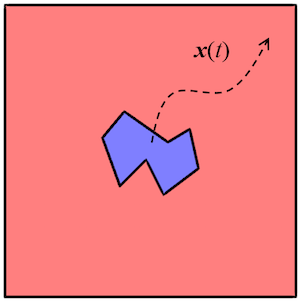
Model Translational Motion with the Deformed Mesh Interfaces
2 interfaces for manually defining the deformation of finite element mesh: Deformed Geometry and Moving Mesh. Learn when and how to use each in this blog post…
