Theory of Thermoviscous Acoustics: Thermal and Viscous Losses

When sound propagates in structures and geometries with small dimensions, the sound waves become attenuated because of thermal and viscous losses. More specifically, the losses occur in the acoustic thermal and viscous boundary layers near the walls. This known phenomenon needs to be considered to evaluate how these losses affect thermoviscous acoustics systems in order to build accurate models and match experimental measurements.

An Introduction to Thermoviscous Acoustics

When modeling the response of small transducers, like condenser microphones, MEMS microphones, and miniature loudspeakers, it is necessary to include thermal and viscous losses. Other applications include analyzing feedback in hearing aids and mobile devices as well as studying the damped vibrations of MEMS structures.

Analyzing the transfer impedance of the standard IEC 60318-4 occluded ear canal simulator, sometimes referred to as the 711 coupler, is a good example to demonstrate the simulation of a thermoelectric device, and is depicted in the figure below. In the graph to the right, the response is modeled with and without thermoviscous acoustic losses. It is evident that these types of losses need to be included in a simulation in order to capture the correct behavior when comparing the curves to the standard data.

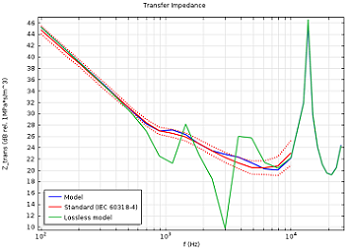
The pressure distribution inside an occluded ear canal simulator at 7850 Hz (left), complying with the IEC 60318-4 standard. The modeled transfer impedance of the coupler is shown in blue, including thermal and viscous losses, together with the prescribed standard curves in red and the curve resulting from a pure lossless model in green (right).

The thermoviscous effect is typically most pronounced at resonances, broadening them and shifting them down in frequency. To model these effects, it is necessary to include thermal conduction effects and viscous losses explicitly in the governing equations, solving the momentum through the Navier-Stokes equations), mass (continuity), and energy conservation equations. This is achieved by solving the thermoviscous acoustics equations in the Thermoviscous Acoustics interfaces in the Acoustics Module. The equations are also known as the viscothermal acoustics or the linearized Navier-Stokes equations.

Here, we will present the physical background for the thermoviscous acoustics equations along with the important boundary layer characteristic: length scale. We will also provide a short description of the material parameters necessary for describing fluid media.

Exploring the Physics Behind Thermoviscous Acoustics

Acoustic waves are the propagation of small linear fluctuations in pressure on top of a background stationary (atmospheric) pressure. The governing equations for the fluctuations (the wave equation or Helmholtz’s equation) are derived by perturbing, or linearizing, the fundamental governing equations of fluid mechanics, including the Navier-Stokes equations, momentum equation, continuity equation, and energy equation. This results in the conservation equations for momentum, mass, and energy for any small (acoustic) perturbation.

For many acoustics simulation applications, a series of assumptions are then made to simplify these equations. The system is assumed lossless and isentropic (adiabatic and reversible). Yet, if you retain both the viscous and heat conduction effects, you will end up with the equations for thermoviscous acoustics that solve for the acoustic perturbations in pressure, velocity, and temperature.

Deriving the Governing Equations

The procedure to derive the governing equations in the frequency domain starts with assuming small harmonic oscillations about the steady background properties. The dependent variables take the form

where p is the pressure, \mathbf{u} is the velocity field, T is the temperature, and \omega is the angular frequency.

Primed (‘) variables are the acoustic variables, while variables accompanied with the subscript 0 represent the background mean flow quantities.

In thermoviscous acoustics, the background fluid is assumed to be quiescent so that \mathbf{u}_0=\mathbf{0}. The background pressure p_0 and background temperature T_0 need to be specified (they can be functions of space T_0=T_0(\mathbf{x}) and p_0=p_0(\mathbf{x})). Inserting the above equation into the governing equations and only retaining terms that are linear in the first-order variables yields the governing equations for the propagation of acoustic waves, including viscous and thermal losses.

Note: Details on this process can be found in the User’s Guide of the Acoustics Module in the “Theory Background for the Thermoviscous Acoustics Branch” section.

The governing equations in the Thermoviscous Acoustics interface, in the frequency domain, are the continuity equation (omitting primes from all the acoustic variables)

where \rho_0 is the background density; the momentum equation

where \mu is the dynamic viscosity, \mu_\textrm{B} is the bulk viscosity, and the term on the right-hand side represents the divergence of the stress tensor; the energy conservation equation

where C_p is the heat capacity at constant pressure, \textrm{k} is the thermal conductivity, \alpha_0 is the coefficient of thermal expansion (isobaric), and Q is a possible heat source; and finally, the linearized equation of state, which relates variations in pressure, temperature, and density

where \beta_T is the isothermal compressibility.

The left-hand sides of the governing equations represent the conserved quantities: mass; momentum; and energy (actually, entropy). In the frequency domain, multiplication with i\omega corresponds to differentiation with respect to time. The terms on the right-hand sides represent the processes that locally change or modify the respective conserved quantity. In two of the equations, diffusive loss terms are present, due to viscous shear and thermal conduction. Viscous losses are present when there are gradients in the velocity field, while thermal losses are present when there are gradients in the temperature.

Viscous and Thermal Boundary Layers

When sound waves propagate in a fluid bounded by walls, so-called viscous and thermal boundary layers are created at the solid surfaces. At the wall, the no-slip condition applies to the velocity field, \mathbf{u} = 0, and an isothermal condition for the temperature, T = 0. The isothermal condition is a very good approximation, as thermal conduction is typically orders of magnitude higher in solids than fluids. These two conditions give rise to the acoustic boundary layer, which consists of the viscous and thermal boundary layers. The flow transforms from the bulk condition of being nearly lossless and described by isentropic (adiabatic) conditions to the conditions in this layer.

The problem of a time-harmonic wave propagating in the horizontal plane along a wall (this could be waves propagating in a small section of a pipe) is illustrated in the figures below. The left figure shows the velocity amplitude, the right figure shows the fluid’s temperature variations from the wall towards the bulk, while the middle figure shows the velocity magnitude as well as an animation indicating the velocity vector over a harmonic period.

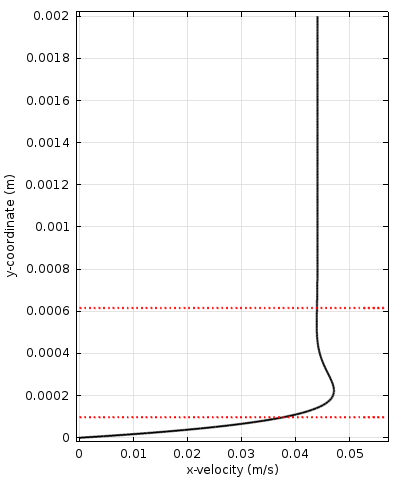
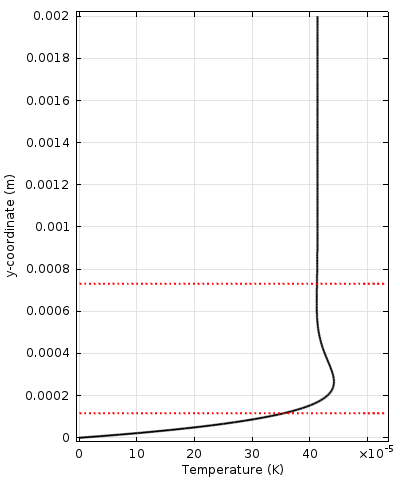
Velocity amplitude (left) and fluid temperature (right), from the wall to the bulk, of an acoustic wave propagating in the horizontal plane (bottom). The viscous and thermal boundary layer thicknesses are indicated by the red dotted lines closest to the wall. The upper dotted lines represent 2 \pi times the boundary layer thickness, in each case. The animation indicates the acoustic velocity components, while the color plot shows the velocity amplitude.

The viscous and thermal boundary layers are clearly visible. The thicknesses are sometimes referred to as the viscous and thermal penetration depths. Because gradients are large in the boundary layer, losses are large here too. This means that in systems of relatively small dimensions, the losses associated with the boundary layer become important. In many engineering applications (miniature transducers, mobile devices, and more), including the losses associated with the boundary layer is essential in order to model the correct physical behavior and response.

The viscous characteristic length is shown as a red dotted line in the velocity and temperature plots shown above, together with 2 \pi times the value (known as the viscous/thermal wavelength). The two characteristic lengths are related by the dimensionless Prandtl number, Pr

which gives a measure of the ratio between the viscous losses and the thermal losses in a system. For air, this number is 0.7, while it is around 7.1 for water. In air, the thermal and viscous effects are roughly equal in importance, while for water (and most other fluids), the thermal losses only play a more minor role. The viscous and thermal boundary layer thicknesses exist as predefined variables for use in postprocessing in the Acoustics Module, and they are denoted by ta.d_visc and ta.d_therm. The Prandtl number is denoted by ta.Pr.

The plane wave problem can be solved analytically and expressions for the viscous (d_\textrm{visc}) and thermal (d_\textrm{therm}) boundary layer thicknesses can be subsequently derived. They are given by

The value of d_\textrm{visc} is 0.22 mm for air and 0.057 mm for water at 100 Hz, 20 °C and 1 atm. The figures below show the viscous and thermal boundary layers over a range of frequencies.

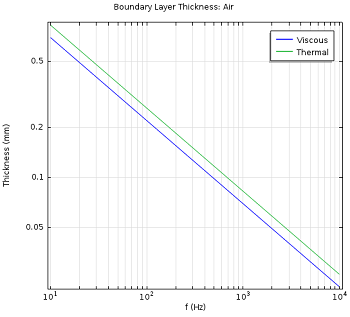
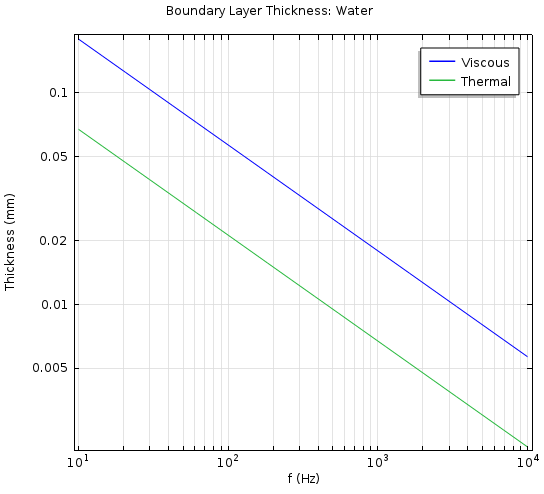
The value of the viscous (d_\textrm{visc}) and thermal (d_\textrm{therm}) boundary layer thicknesses as functions of frequency for air (left) and water (right).

This shows the diminishing effect of viscous and thermal losses at increasing acoustic wave propagation frequencies. Finally, another important effect that is captured when modeling with the Thermoviscous Acoustics interface is the transition from adiabatic to isothermal acoustics at low frequencies in small devices. This effect occurs when the thermal boundary layer stretches over the full device and is important in, for example, condenser microphones, such as the B&K 4133 condenser microphone. At isothermal conditions, the speed of sound changes to the isothermal speed of sound.

Bulk Losses, Attenuation, and Narrow Region Acoustics

It is important to note that viscous and thermal losses also exist in the bulk of the fluid. These are losses that typically occur when acoustic signals propagate over long distances and are attenuated. One example of this is sonar signals. These types of losses are, in air, only dominating at very high frequencies (they can be neglected at audio frequencies). The bulk losses are, of course, also described by the governing equations for thermoviscous acoustics as they include all of the physics. However, modeling large domains with the thermoviscous acoustics equations is very computationally expensive. In the Acoustics Module, you should instead use the Pressure Acoustics interface and select one of the available fluid models: Viscous, Thermally conducting, or Thermally conducting and viscous.

Modeling with the Thermoviscous Acoustics interface can be computationally expensive because of the details needed to capture all physical effects. In cases where the acoustics waves propagate in waveguides or ducts of constant cross section, the thermoviscous losses can be modeled using the Narrow Region Acoustics feature in the Pressure Acoustics, Frequency Domain interface. This domain feature adds the losses associated with the acoustic boundary layers to the fluid in a homogenized way. The losses are derived analytically, thus exact for this case. This feature is very useful to reduce model size or quickly get a first assessment of results before moving onto a full and detailed thermoviscous model.

Material Parameters

Solving a full thermoviscous acoustics model involves defining several material parameters:

• Dynamic viscosity, \mu
  • The dynamic viscosity \mu measures the fluid’s resistance to shearing in the fluid. It is the constant that relates stress to velocity gradients. The dynamic viscosity is related to the kinematic viscosity \nu by the relation \mu = \rho_0 \: \nu. The symbol for the dynamic viscosity \eta is also sometimes used.
• Bulk viscosity, \mu_\textrm{B}
  • The bulk viscosity is also known as the volume viscosity, second viscosity, or expansive viscosity. It is related to losses that appear due to the compression and expansion of the fluid. \mu_\textrm{B} appears in the stress tensor term (right side of equation 3), which has to do with the compressibility (\nabla\cdot\mathbf{u}) of the bulk fluid. This factor is difficult to measure and often depends on the frequency.
• Heat capacity at constant pressure (specific), C_p
  • This material parameter measures how much energy is required to change the temperature of the fluid (at constant pressure).
• Coefficient of thermal conduction, \textrm{k}
  • The coefficient of proportionality between the temperature gradient and the heat flux in Fourier’s heat conduction law.
• Coefficient of thermal expansion (isobaric), \alpha_0
  • This is the volumetric thermal expansion of the fluid and expresses the ability of the fluid to expand when its temperature rises.
• Isothermal compressibility, \beta_T
  • An important parameter in the equation of the state of the fluid. It relates changes in pressure to changes in volume in the fluid. The isothermal compressibility is related to the usual (isentropic) compressibility through the ratio of specific heats by \beta_T = \gamma \beta_s.

Concluding Thoughts on the Theory of Thermoviscous Acoustics

Now that we have discussed the theory behind thermoviscous acoustics and the associated equations, we can move on to tips and tricks for setting up a thermoviscous acoustics model using COMSOL Multiphysics and the Acoustics Module. We will discuss this, as well as many examples and applications, in the next blog post in this series.

Further Reading and References

• The “Thermoviscous Acoustics Branch” section in the Acoustics Module User’s Guide of the COMSOL Documentation
• D. T. Blackstock, “Fundamentals of Physical Acoustics”, John Wiley and Sons, 2000
• S. Temkin, “Elements of Acoustics”, Acoustical Society of America, 2001
• B. Lautrup, “Physics of Continuous Matter”, Second Edition, CRC Press, 2011
• P. M. Morse and K. U. Ingard, “Theoretical Acoustics”, Princeton University Press
• A. D. Pierce, “Acoustics: An Introduction to Its Physical Principles and Applications”, Acoustical Society of America, 1989
• A. S. Dukhin and P. J. Goetz, “Bulk viscosity and compressibility measurements using acoustic spectroscopy”, J. Chem. Phys. 130, 124519 (2009)

Editor’s note: This blog post was updated on 7/12/2016 to be consistent with version 5.2a of COMSOL Multiphysics.