Discussion Closed This discussion was created more than 6 months ago and has been closed. To start a new discussion with a link back to this one, click here.
How to adjust the weighting factor of a multi-objective function so that the objective function transitions naturally
Posted Sep 29, 2023, 2:03 a.m. EDT Fluid & Heat, Computational Fluid Dynamics (CFD), Optimization Version 6.0 3 Replies
Please login with a confirmed email address before reporting spam
Dear Mr./Miss.,
In topology optimization, ually the multi-objective function is of the form: obj=wobj1+(1-w)obj2. Adjusting the weighting factor w is able to obtain the optimization curve of the design. In the research work of others, transition of the whole topology is obvious and clear as w is incremented or decremented, shown in Fig. 1
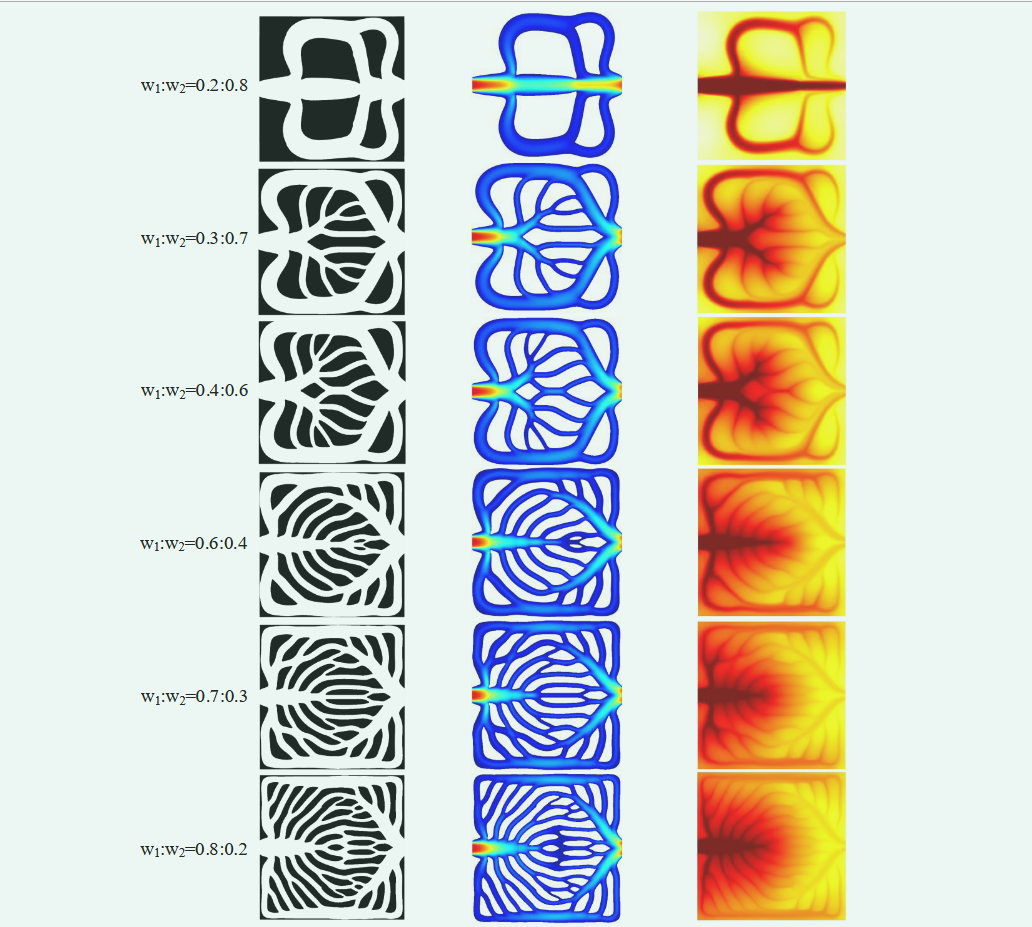However, in my topology optimization structure, the problem of adjusting the weight factor transition is not obvious, as shown in Fig. 2.
When w=0.5, the overall topology is very much inclined to flow rather than equalizing flow and heat transfer. It is worth noting that I have normalized obj1 and obj2 before optimization. If obj1=Ere/Ebase, Ere refers to the flow dissipation after optimization and Ebase values the flow dissipation in the initial state.
So my question is, what are those parameters I need to adjust or observe in order to adjust the weight factors to get the proper topology. Also what do I need to do to perform the prior sensitivity analysis for topology optimization in comsol?
Best regards, Gavin.
Please login with a confirmed email address before reporting spam
Hi,
The sensitivity analysis needed for topology optimization happens automatically, so you do not need to do anything.
I do not understand the question. What do you mean by "proper topology"? The optimized design depends on several non-dimensionless number (not only w). Both the Darcy and Péclet number can affect the result.
Some problems will benefit from using movelimits with MMA. This setting is available on the topology optimization study step.
Best regards,
Kristian E. Jensen
Technical Product Manager, Optimization
Please login with a confirmed email address before reporting spam
Dear Jensen Thank you very much for your kind instruction. A proper topology optimization implies that the objective function tends to flow or heat transfer smoothly as the weight factor w is increasing or decreasing. When w=0.5, there should be balanced flow and heat transfer, and in my optimization process, the topology result at this point is clearly more inclined to flow. This leads to a simpler overall topology after w>0.5. At the same time, I am a bit confused about the effect of Pe number on the results. Does it mean that with a larger Pe number, the overall forced motion is more inclined to convection than diffusion?Or how do I need to adjust the Pe number. Also how do the movement limits need to be set in the MMA method, is there an official Comsol case, thanks. Best regards, Gavin.
Please login with a confirmed email address before reporting spam
You can set the movelimit on the topology optimization study step, but I do not think it will help.
The topology optimization minimizes the objective while respecting the constraints. I guess you have a flow driven setup in this case and use the pressure loss as one of the objectives. You then expect to get a similar objectives for w=0.5, but the problem is nonlinear so there is no reason that this should happen. If you like, you can use pressure driven setup instead to avoid the w alltogether.
The results you show seem to reproduce the behavior presented in the paper in a qualitative sense. The remaining differences can be due to many things: variations in numerical and/or physical parameter or perhaps a different mesh/discretization.
Best regards,
Kristian E. Jensen
Technical Product Manager, Optimization