Technical Papers and Presentations

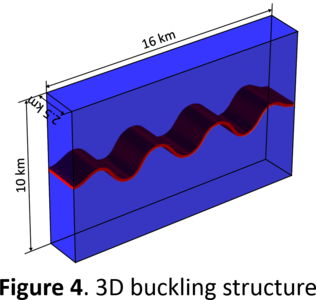
COMSOL Multiphysics^® is used in various engineering fields and has recently been introduced as an efficient tool to solve certain geophysical problems. We used this software to study the mechanisms associated with the buckling formation at a plate-tectonic scale on Earth. Buckling is not only important in geophysics but is also a phenomenon that has significance in other research fields, such as architectural and mechanical engineering. In terms of structural geology, a buckling structure can form due to compression when a high-strength layer is embedded in a weak matrix. In nature, buckling structures occur over a wide size range, from within small quartz grains to the mantle scale. The Earth’s lithosphere is a layered structure with varying mechanical strengths, existing predominantly under a compressional regime, which allows the lithosphere to form a buckling structure. The various characteristics of a buckling structure (e.g., wavelength, amplitude, and orientation) are indicators with which we can estimate the lithospheric stress (e.g., the magnitude and direction) and buckling initiation environment. Here, we built a viscoelastic numerical model with a thin embedded layer inside a rectangular domain, which has an area of several hundred km². For the high-strength embedded layer, the Young's modulus and viscosity were set to 100 GPa and 10²³ Pa.s, respectively, where the mechanical properties of the surrounding matrix also changed with the viscoelastic contrast. Previous studies on buckling based on numerical experiments were performed at a small spatial scale and low strength. Therefore, it is difficult to apply these previous results to a realistic lithospheric buckling scenario. In this study, we applied higher strength and larger scale to simulate a realistic lithosphere buckling structure. We adopted a Lagrangian approach, which can deform the model geometry and mesh. Since we assume that the material is a viscoelastic solid, we used a Solid Mechanics interface in COMSOL Multiphysics^®. We used a Time Dependent solver because the numerical model is compressed with a constant velocity over time. To quantify the effect that various factors have over the control of buckling, such as the strength contrast, the thickness of the embedded layer, and the parameters, we applied the Parametric Sweep. We used a rectangle element with 4 nodes provided by the software and applied a small-sized mesh near the high strength layer. Here, we observed that larger strength contrasts, as well as increased thicknesses of the strong layer, results in increased wavelengths and amplitudes in the buckling structure. Our results are reliable because trends identical to the theoretical buckling mechanism were obtained from the viscous materials of many previous numerical studies. Based on these results, we argue that COMSOL Multiphysics^® is a useful tool to understand lithospheric buckling physics over a wide range of shallow to deep Earth situations.