Modeling of the Viscous Flows in a Network of Thin Tubes
Flows in thin tubes arise in a wide variety of contexts like microfluidics and flows in blood vessels. Stationary laminar incompressible viscous flows in a thin tube were studied empirically and theoretically in the nineteenth century. They are described by the stationary Poiseuille profile. However, the time scale of the phenomena may prevent stationary approximation to be valid as noticed by Womersley for blood flows. In that case, one needs to use a time-dependent Poiseuille profile.
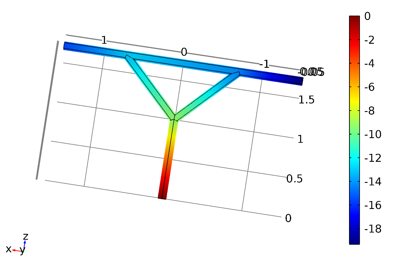
An asymptotic analysis of the time dependent three dimensional Navier-Stokes equation in a thin tube structure [1,2] leads to two types of equations for the pressure on the graph of the structure. One of them is a well-known Reynolds equation on the graph with Kirchhoff junction conditions at the nodes (it appears at the slow time scale); another equation is a new one proposed by G.Panasenko and K.Pileckas in [1, 2]. It couples a one-dimensional, nonlocal in time problem on the graph with a heat equation in the cross-section of the tubes. We investigate numerical schemes for this problem. We also compare numerically this asymptotic model with the directly numerically solved full 3D nonstationary Navier-Stokes equations. Simulations were performed with COMSOL Multiphysics® software using the CFD Module to analyze the pressure and velocity profile in tubes. The full dimension Navier-Stokes simulations were run on different geometries (Fig.1).
Simulations with COMSOL Multiphysics® software run over the time interval [0; 0:0875ε2] for ε ϵ {0.2; 0.1; 0.05; 0.025}. We show in Figures 2 and 3 the velocity magnitude and the pressure inside tubes structure for ε=0.1. Notice that the velocity magnitude is not convex in the cross-section, unlike the stationary Poiseuille profile. According to [2], the junction boundary layers have a space width of order of ε. The asymptotic model shows a good agreement with Navier-Stokes numerical solution, with only 6% error when ε = 0.025 in the multiply connected geometry case and 1% error when ε ≤ 0.1 in the simply connected geometry case.
This research might be useful to reduce the computational complexity in certain hemodynamical problems.
[1] Panasenko G., Pileckas K., Asymptotic analysis of the non-steady Navier-Stokes equations in a tube structure.I. The case without boundary layer-in-time. Nonlinear Analysis, Series A, Theory, Methods and Applications, 122, 2015, 125-168, http://dx.doi.org/10.1016/j.na.2015.03.008
[2] Panasenko G., Pileckas K., Asymptotic analysis of the non-steady Navier-Stokes equations in a tube structure. II. General case. Nonlinear Analysis, Series A, Theory, Methods and Applications, 125, 2015, 582-607, http://dx.doi.org/10.1016/j.na.2015.05.018
[3] Canon É., Chardard F., Panasenko G., Štikonienė O., Numerical solution of the viscous flows in a network of thin tubes. (Submitted 2019)