Technical Papers and Presentations

When an electronic device is worn for extended periods, possibly in direct contact with human skin, heat must be safely transferred away from the device, without exceeding standards and regulatory temperature limits on the skin and on the exposed surfaces of the device. Heat transfer is dominated by convective heat transfer to the surrounding air (possibly trapped air under clothing), and by blood flow cooling. This presentation will discuss each of these two mechanisms, including how to calculate and directly (non-iteratively) apply a “user-defined” convective heat transfer coefficient, allowing more flexibility than the built-in external and internal convection options in COMSOL Multiphysics® software.

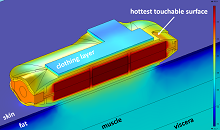
Figure 1 shows a cut-away view of a human body and an example of an electronic device in direct contact with the skin. Color represents temperature as calculated by COMSOL. Note that there is a clothing layer on top of the device and above the skin, trapping air under the clothing. (The clothing is only shown on top of the device, and only a portion is shown.) To calculate the temperatures correctly, it is essential that all convective heat transfer (from skin to trapped air, from device to trapped air, from clothing to ambient air) are handled properly.

COMSOL has several choices of built-in heat transfer coefficients that work well as boundary conditions in most situations. However, in this example we desire greater control of the calculations and select a “user defined” heat transfer coefficient that we specify. Instead of specifying a fixed number, we calculate the coefficient by explicitly defining four dimensionless numbers, the Nusselt, Rayleigh, Grashof, and Prandtl numbers as variables in COMSOL, and calculating the convective heat transfer coefficient from these. The calculated heat transfer coefficient is itself a variable, and cannot be directly specified as the heat flux boundary condition (this would effectively cause a circular definition). Instead, we define an extra equation that ensures that the difference between the calculated coefficient and the specified coefficient is zero. For the benefit of beginner COMSOL users – who may be unfamiliar with the Global ODE node – the presentation will show how to do this.

Figure 2 compares the temperature as a function of distance to the skin, with or without the device present. (With the device present the temperature is taken directly under the center of the module.) Note the almost flat temperature profile from 3 cm and further into the body, as would be expected in a real body. The flat profile is the consequence of including heat transfer by blood flow.