Technical Papers and Presentations

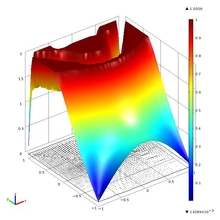
We treat a gradient constrained minimization problem which has applications in mechanics and superconductivity. A particular case of this problem is the elastoplastic torsion problem. In order to solve the problem we developed an algorithm in an infinite dimensional space framework using the concept of the generalized Newton derivative.

The Desktop environment of COMSOL Multiphysics 4.1 was used to test the algorithm with Argyris finite elements. For the implementation of Newton iterations we used time-discrete solver for it was convenient with it to pass the gradient data from iteration to iteration by using of the \'prev\' operator. Numerical tests demonstrate mesh-independent behaviour of the method.