Technical Papers and Presentations

Using the COMSOL Multiphysics® software with the Heat Transfer Module, we calculated coupled heat and moisture transport to simulate the amount and distribution of condensed moisture in a train wall, with a special focus on the surface of thermal bridges. We tested two approaches to calculate the thickness of a condensate layer forming where the cold surface of a thermal bridge is in direct contact with the warm and moist cabin air:

1. Using the multiphysics node “Heat and Moisture Transport in Building Materials”, the air can be considered as a building material, with an artificially defined moisture content increasing sharply for relative humidities approaching 100%. This artificially large vapor capacity is a mathematical trick rather than a physical reality. It makes the air layer accumulate moisture on the surface of a thermal bridge where the relative humidity is close to 100%, and hence allows for the calculation of a layer thickness from the volume integral of the moisture content.

2. The presence of a condensate layer is simulated by limiting the relative humidity on the thermal bridge surface to 100% and by keeping it at 100% for as long as a condensate layer is present. These boundary conditions are implemented by means of two weak inequality conditions. The vapor flux consistent with these conditions can be used to formulate an ODE for the thickness of the condensate layer which is coupled to the standard differential equations for heat and moisture transport and solved simultaneously.

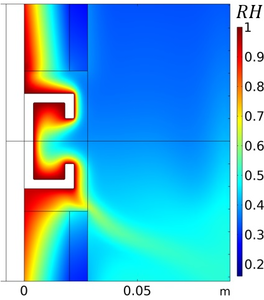
In both approaches the condensate layer is not physically implemented in the model, but a purely mathematical quantity. This has the advantage of simple geometry and meshing. The two approaches proved consistent in a 1-dimensional test scenario. For the 2- and 3-dimensional simulations of thermal bridges we used the second approach because it allows convective transport to be taken into account, which is the dominant mechanism of moisture transport to the surface of thermal bridges in vertical train walls.

The results suggest that in a cold winter scenario, enough water condenses onto thermal bridges exposed to convective air flow to form draining drops within some hours. The simulation of evaporating layers proved difficult with the aforementioned methodology, because the ODE for the condensate layer thickness enforced very small solver time steps.