Learning Center

More on Deep Neutral Network Surrogate Models

---

Neural network optimizers are used for training neural networks by adjusting the model parameters to minimize the loss function. These optimizers are based on stochastic gradient descent (SGD) techniques, where randomness in data selection helps improve generalization and efficiency. Here, we give an overview of the network optimizer and cover hyperparameters such as learning rate, batch size, and number of epochs, which are used for the training and validation process. Part 2 continues this discussion of deep neural networks with detailed information on activation functions.

Neural Network Optimizers

The solver algorithm used for training neural networks is a type of stochastic gradient descent method. Note that several names are used interchangeably: method, solver, algorithm, and optimizer. The stochastic aspect refers to the random selection of data points that are used to compute the gradient of the loss function (objective function). Instead of using the entire dataset to compute the gradient of the loss function, a stochastic gradient descent method randomly selects one data point at a time or, more commonly, a small subset called a mini-batch, to perform an update on the network parameters.

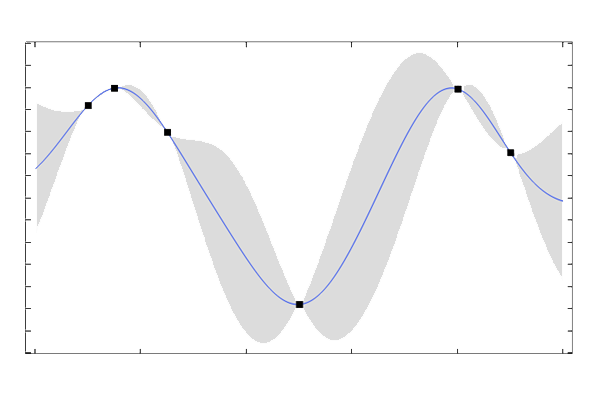
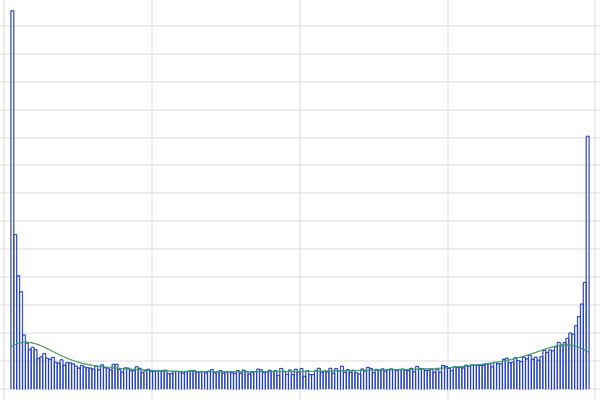
In a mini-batch method, a small batch, typically between 10 and a few hundred data points, is randomly selected from the dataset. The gradient of the loss function is then computed using this mini-batch rather than the full dataset or an individual data point. The randomness in selecting data points introduces variability in the gradient estimates, which helps escaping local minima in the loss landscape, potentially leading to better generalization on unseen data. As a result, the updates to the network parameters are noisy, as can be seen from the convergence plots. These stochastic updates generally make the method faster for large datasets, as it doesn't require the entire dataset to be loaded into memory and processed for each iteration.

The convergence of a stochastic gradient descent solver tends to be noisy.

The default stochastic gradient descent solver is the Adam optimizer, which stands for Adaptive Moment Estimation. A nonadaptive stochastic gradient descent optimizer is also available as the SGD option from the Method list in the user interface. The Adam optimizer enhances the SGD method by computing individual adaptive learning rates for different parameters. This is based on estimates of first and second moments of the gradients; in other words, the optimizer considers both the average and the variance of the gradients to adjust the learning rates. With this adaptive adjustment, the Adam optimizer is more effective in handling sparse gradients and different scales of data, which are common challenges in training deep neural networks. The Adam optimizer also typically converges faster than SGD because of these adaptive adjustments.

Training and Validation Settings

The Training and Validation section of the Deep Neural Network function Settings window contains the solver parameters, also known as hyperparameters, and validation settings.

The Training and Validation section of the Deep Neural Network function Settings window.

Some of the most important solver parameters (not to be confused with the network parameters: weights and biases) in the Training and Validation section are the Learning rate, Batch size, and Number of epochs.

• The Learning rate, which can be likened in some ways to numerical damping in a nonlinear Newton solver, determines the step size during the optimization process. A learning rate that is too small can lead to the model getting stuck in a local minimum, while a learning rate that is too large can result in overshooting the minimum and poor convergence.
• The Batch size denotes how the training data is divided up into subsets during the optimization process. A batch size that is too small can lead to noisy gradient updates and longer training times, while a batch size that is too large might lead to poor generalization and inefficient utilization of computational resources.
• The Number of epochs, which defines the number of complete passes through the entire dataset, plays an important role in the learning process. Too few epochs can result in underfitting, where the model has not adequately learned from the training data, while too many epochs can lead to overfitting, where the model learns the noise in the training data and performs poorly on new, unseen data.

The Validation data setting lets you choose how the fraction of validation data is selected as well as the size of the validation data sample. In addition, there are Random seed settings both for the optimizer and the validation data selection.

The Validation data options.

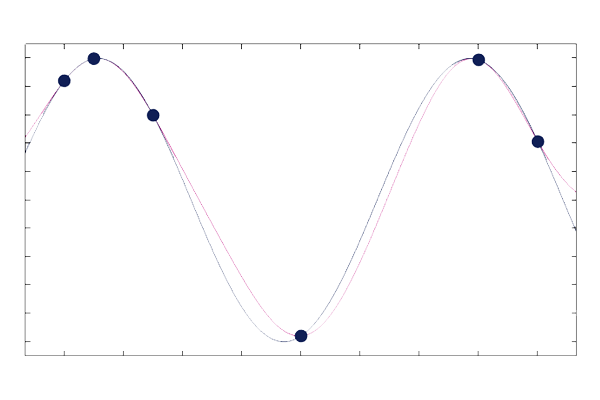
Visualization of an overfitted model.

Visualization of a well-fitted model.

Network Architectures

The Deep Neural Network (DNN) function in COMSOL Multiphysics^® is a so-called dense feed-forward network. A DNN model consists of an input layer, a series of hidden layers, and an output layer. Each layer consists of a number of nodes, or neurons. Choosing the number of layers and nodes in a neural network is often an iterative process that involves a combination of knowledge about the specific problem and data, empirical testing, and a bit of trial and error. A network with too few hidden layers or nodes may not be complex enough to serve as an accurate surrogate model. A network with too many hidden layers or nodes may suffer from so-called overfitting, where the network performs well on the training data but fails to generalize to a dataset that it was not trained on. A model with a large number of hidden layers or nodes will also be slower to evaluate than a lighter model with fewer layers or nodes.

The figure below shows a few network configurations that can serve as inspiration for your own surrogate modeling projects.

Typical neural network architectures, including the input layer (cyan nodes on the left), hidden layers (blue nodes in the middle), and output layer (cyan nodes on the right).

Surface Regression

With regard to identifying an optimal network architecture for the surface regression task in Part 2, z=f(x,y), the neural network configuration is shown to be effective. Initially, we used a smaller network with the architecture , which performed reasonably well. Based on this, we scaled the network up to improve performance. In practice, it's common to experiment with various configurations, such as and , among others. The use of powers of two, or a multiple of the number of inputs, for the number of neurons is a traditional approach, but other values can also be used.

The final choice of a network starts with two input neurons matching the function's inputs, expands to capture complex patterns through a peak of 64 neurons, and then narrows down, which helps in refining and summarizing the learned features before reaching the single output. This structure enables the network to learn both simple and complicated relationships within the data, providing a good mix of depth and complexity for handling nonlinearities and interactions effectively without being at risk of overfitting. This makes it suitable for regression tasks where both accuracy and generalization are needed.

Deep Neural Network Example Applications

There are tutorial models available in the Application Libraries and Application Gallery that demonstrate the use of different deep neural network configurations. For the Tubular Reactor Surrogate Model application, available in the Application Libraries, the input parameters include coordinate values alongside model parameter values, which represent relatively feature-rich inputs. There are two outputs for the temperature and a reaction quantity. In this case, a network with the architecture is used. The first layer expanding to 50 neurons enables the network to capture a wide range of interactions and dependencies among the inputs, capturing the complicated nonlinear behaviors of the reactor. Subsequent layers (40, 30, 20) progressively refine these features, focusing on the most relevant aspects that impact the outputs, ensuring that the network learns the most critical patterns from the simulation data.

In a similar manner, the following, more advanced, version of the Thermal Actuator Surrogate Model application, uses a network architecture of .

Typical DNN Architectures and Choosing

The most common network architectures often have a funnel-like design, where the layers initially increase in size to expand the feature space and then decrease to distill these features into a more compact form. This process can be viewed as a form of compression, where the neural network identifies and abstracts relationships in the data into a minimalistic representation. From this perspective, the architecture of the network works as a sophisticated filter, successively refining the input data into increasingly useful forms, ultimately focusing on the most characteristic features that are needed for the task.

The number of neurons in the layers should typically reflect the number of inputs and outputs. A higher number of inputs usually requires more neurons in the first hidden layer. Similarly, a higher number of outputs often requires more neurons in the last hidden layer to ensure that the network can differentiate and provide sufficient information for each output. The rest of the network should be scaled accordingly.

In general, it is hard to realize, without trial and error, which network architecture to choose. As a rule of thumb, start with a simple network, such as in the first example above having a network. Then, successively increase the number of nodes of each layer, and if this is not enough, increase the number of layers as well.

Note that adding output parameters, and thereby output nodes, will affect the training convergence. Adding an output parameter can improve or worsen the convergence of a neural network. Additional outputs provide more training signals, potentially improving convergence. However, they also increase complexity and computational demands.

Network Parameters

When the optimizers are run for training a neural network, the values for the weights and biases of the network are optimized to fit the data as closely as possible. The network weights are factors that influence how much each input affects the output. The network biases allow the network model to adjust the output along with the weighted inputs to better match the data. The biases are associated with the hidden layer nodes as well as the output layer nodes, while the weights are associated with the edges in the network graph. In the figure below, a network is presented as a graph with labels for all the biases and some of the weights.

A column containing two cyan circles, a column containing four dark blue circles, a column of eight dark blue circles, another column of four dark blue circles, and then a column containing one cyan circle, which are connected through a series of lines and show a mesh-like structure as well as many text labels annotated next to certain lines and in every circle.

A neural network with labels for the biases and some of the weights.

The number of network parameters — the sum of the number of weights and biases — can be used to assess the computational complexity of a neural network. In the Deep Neural Network function Settings window, after training is finished, the total number of parameters are displayed in the Information section. In the case of the network, the number of network parameters is 93.

To manually compute the number of network parameters in the case of the larger network, we can proceed as follows:

• Input Layer: 2 inputs
• Hidden Layer 1: 32 nodes
  • Weights: Each node (or neuron) in the first hidden layer is connected to all inputs. So, there are 2 — 32=64 weights.
  • Biases: There is one bias per node, so there are 32 biases.
• Hidden Layer 2: 64 nodes
  • Weights: Each node in the second hidden layer is connected to all nodes in the first hidden layer. So, there are 32 — 64=2048 weights
  • Biases: There is one bias per node in the second hidden layer, adding 64 biases.
• Hidden Layer 3: 32 nodes
  • Weights: Each node in the third hidden layer is connected to all nodes in the second hidden layer. So, there are 64 — 32=2048 weights.
  • Biases: There is one bias per node in the third hidden layer, adding 32 biases.
• Output Layer: 1 node
  • Weights: Each node in the output layer is connected to all nodes in the third hidden layer. So, there are 32 — 1=32 weights.
  • Biases: There is one bias at the output node, adding 1 bias.

The number of total parameters equals the number of total weights and total biases:

• Total Weights: 64+2048+2048+32=4192
• Total Biases: 32+64+32+1=129
• Total Parameters: 4192+129=4321

You can check that this number matches the number displayed in the Information node for the network model from Part 2 of the Learning Center course on surrogate modeling.