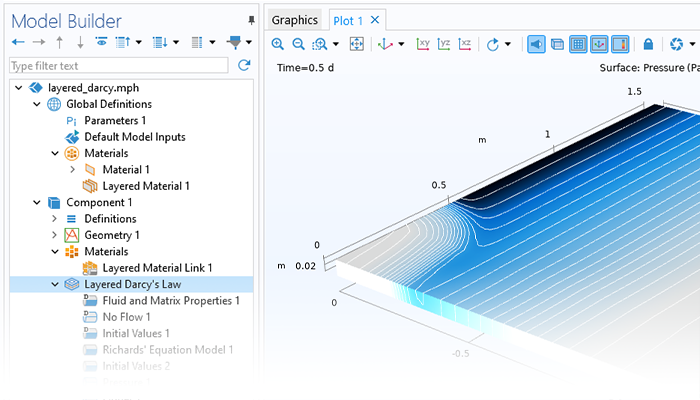
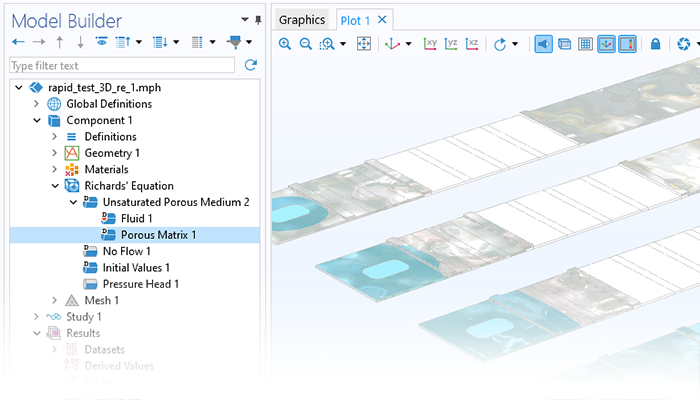
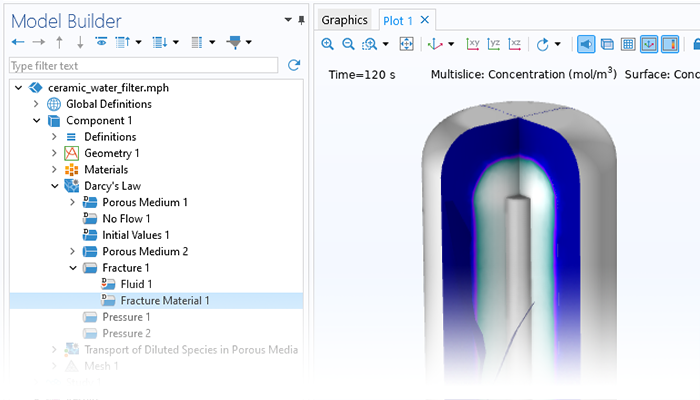
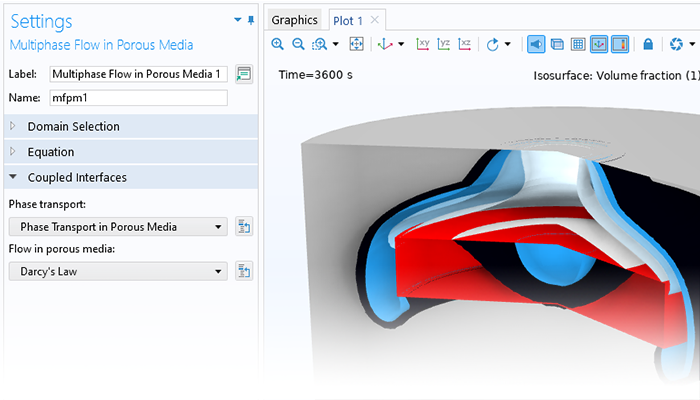
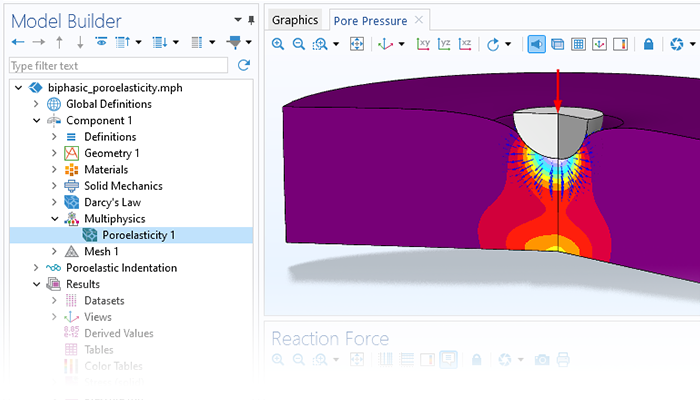
Optimize a Variety of Industrial Processes
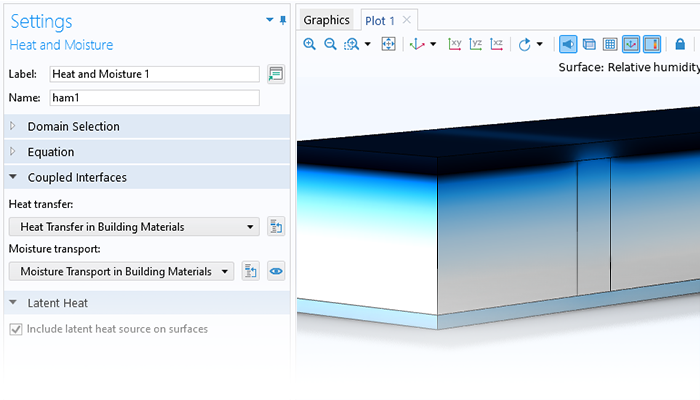
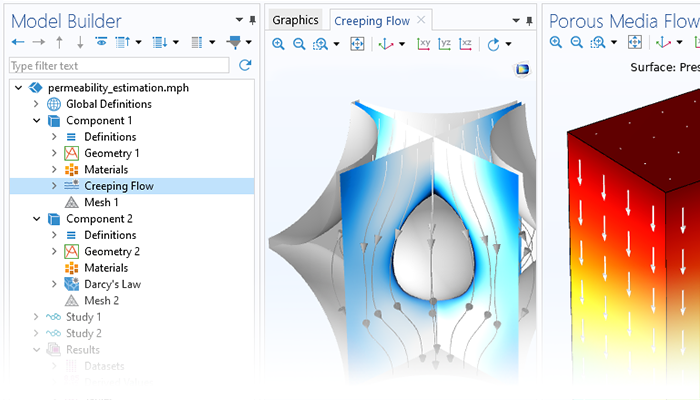
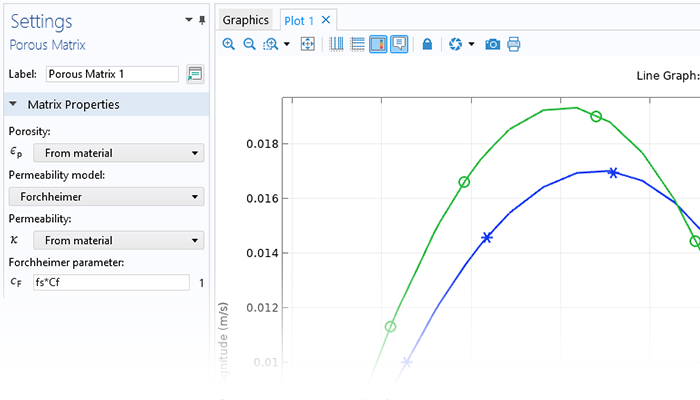
The need for advanced porous media modeling spans many industries and applications, including the pharmaceutical and food industries, for example. The Porous Media Flow Module helps agricultural, chemical, civil, and nuclear engineers and scientists across industries to analyze porous media flows and optimize their designs and processes.
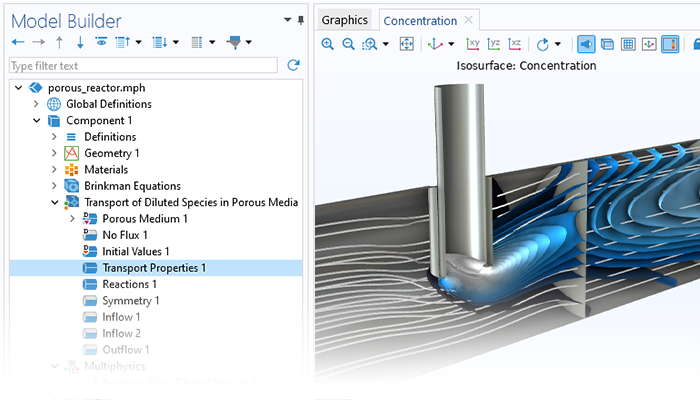
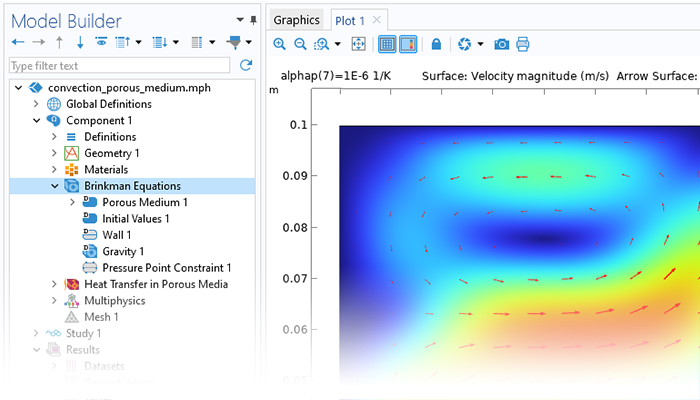
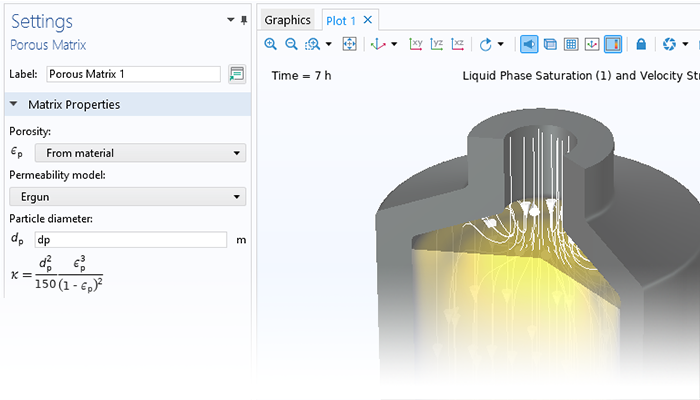
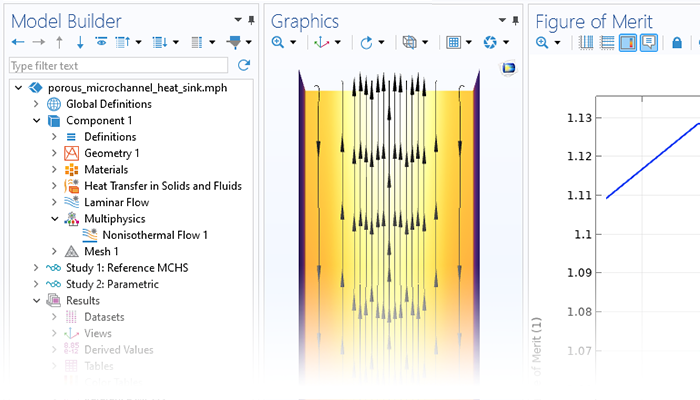
Simulation can be used to capture the effects of porous media on transport processes when modeling nanomaterials, porous reactors, the cooling of electronic components, and large-scale geotechnical applications. COMSOL Multiphysics® provides a comprehensive set of modeling tools that are packaged into physics interfaces, which automatically set up and solve the equations specific to the type of porous media flow you are modeling.